SAS第八课:直线回归、直线相关与Logistic回归(下)
2012-04-17 生物谷 生物谷
§8.4 多元线性回归 REG过程不仅可以完成只有一个自变量的简单直线回归,还可以作含有多个自变量的多元线性回归。作多元线性回归时REG过程的语法格式与简单直线回归的语法几乎完全相同,只要把要分析的多个自变量名放在MODEL语句中应变量后即可。因为多元线性回归时一般要作自变量的筛选,涉及到MODEL语句的选项,现将多元线性回归常用的选项介绍如下: 8.4.1 语法选项 SE
§8.4 多元线性回归
REG
8.4.1 语法选项
- SELECTION=method ,规定变量筛选的方法,method可以是以下几种选项
- FORWARD( 或F),前进法,按照SLE规定的P值从无到有依次选一个变量进入模型
- BACKWARD (或B),后退法,按照SLS规定的P值从含有全部变量的模型开始,依次剔除一个变量
- STEPWISE (或S),逐步法,按照SLE的标准依次选入变量,同时对模型中现有的变量按SLS的标准剔除不显著的变量
- NONE ,即不选择任何选项,不作任何变量筛选,此时使用的是含有全部自变量的全回归模型
- SLE= 概率值,入选标准,规定变量入选模型的显著性水平,前进法的默认是0.5,逐步法是0.15
- SLS= 概率值,剔除标准,指定变量保留在模型的显著水平,后退法默认为0.10,逐步法是0.15
-
标准化偏回归系数
STB 可用来比较各个自变量作用的大小
- COLLIN 要求详细分析自变量之间的共线性,给出信息矩阵的特征根和条件数,来判断自变量之间有无多重共线性。
8.4.2 应用实例
例
8.3 现有20名糖尿病人的血糖(y,mmol/L)、胰岛素(X1,mU/L))及生长素(X2,μg/L)的测量数据列于中,试进行多元线性回归分析(卫生统计第四版例11.1)。20
名糖尿病人的血糖、胰岛素及生长素的测量数据|
病例号 i |
血 糖 y |
胰岛素X1 |
生长素X2 |
|
1 |
12.21 |
15.20 |
9.51 |
|
2 |
14.54 |
16.70 |
11.43 |
|
3 |
12.27 |
11.90 |
7.53 |
|
4 |
12.04 |
14.00 |
12.17 |
|
5 |
7.88 |
19.80 |
2.33 |
|
6 |
11.10 |
16.20 |
13.52 |
|
7 |
10.43 |
17.00 |
10.07 |
|
8 |
13.32 |
10.30 |
18.89 |
|
9 |
19.59 |
5.90 |
13.14 |
|
10 |
9.05 |
18.70 |
9.63 |
|
11 |
6.44 |
25.10 |
5.10 |
|
12 |
9.49 |
16.40 |
4.53 |
|
13 |
10.16 |
22.00 |
2.16 |
|
14 |
8.38 |
23.10 |
4.26 |
|
15 |
8.49 |
23.20 |
3.42 |
|
16 |
7.71 |
25.00 |
7.34 |
|
17 |
11.38 |
16.80 |
12.75 |
|
18 |
10.82 |
11.20 |
10.88 |
|
19 |
12.49 |
13.70 |
11.06 |
|
20 |
9.21 |
24.40 |
9.16 |
|
平均值 |
10.85 |
17.77 |
8.94 |
|
Libname a ‘c:\user’; |
|
data a.bk4_1; |
|
infile ‘c:\user\li4_1’; |
|
input id y x1 x2@@; |
|
proc reg data=a.bk4_1; |
|
model y=x1 x2/stb; |
|
model y=x1 x2/ selection=stepwise stb; |
|
run; |
REG
过程中MODEL语句可以交互使用,本例我们建立了两个模型,第一个model没有作变量筛选,建立一个含有两个自变量的方程,并输出标准化偏回归系数。第二个model指定逐步回归法筛选变量。程序运行的主要结果如下:Model:model1 模型1 Dependent Variable:Y
Analysis of Variance
回归模型的方差分析
Sum of Mean
Source DF Squares Square F Value Prob>F
变异来源 自由度 离均差平方和 均方 F值 P值
Model 2 116.62646 58.31323 21.539 0.0001
Error 17 46.02494 2.70735
C Total 19 162.65140 误差的均方根 Root MSE 1.64540 决定系数 R-square 0.7170
应变量的均数 Dep Mean 10.85000 调整的决定系数 Adj R-sq 0.6837
应变量的变异系数 C.V. 15.16500 Parameter Estimates
以下是参数估计和假设检验(t检验法)
Parameter Standard T for H0: Standardized
Variable DF Estimate Error Parameter=0 Prob > |T| Estimate
变量名 自由度 参数估计值 估计值的标准误Sb t值 P值截距 INTERCEP 1 17.010824 2.47237134 6.880 0.0001 0.00000000
X1 1 -0.405907 0.09412204 -4.313 0.0005 -0.74340924
X2 1 0.097669 0.11588150 0.843 0.4110 0.14528940Model:model2(模型2) Dependent Variable:Y(应变量名)
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F Model 1 114.70324 114.70324 43.060 0.0001
Error 18 47.94816 2.66379
C Total 19 162.65140 Root MSE 1.63211 R-square 0.7052
Dep Mean 10.85000 Adj R-sq 0.6888
C.V. 15.04250Parameter Estimates
Parameter Standard T for H0: Standardized
Variable DF Estimate Error Parameter=0 Prob > |T| Estimate INTERCEP 1 18.796143 1.26472741 14.862 0.0001 0.00000000
X1 1 -0.458520 0.06987466 -6.562 0.0001 -0.83976728
REG
过程拟合带截距项的直线回归方程,用最小二乘法估计模型的参数,并给出模型及参数的方差分析和t检验。本例的两个模型检验P值都小于0.05,模型有统计学意义。模型1含有两个自变量,其截距项和X1检验有统计学意义,X2的检验无统计学意义。模型2为逐步回归法,只纳入了X1。比较两个模型的决定系数,模型1因含有两个自变量,决定系数比模型2要大,但因为模型纳入了不显著的自变量X2,导致它的调整决定系数反而较小,所以我们选择模型2,回归方程:Y=18.796-0.459X1。§8.5 logistic回归
如果应变量为分类的变量,则不符合一般回归分析模型的要求,可用
logistic回归来分析。Logistic回归按反应变量的类型分为:- 两分类的
按照设计类型可分为:
- 非条件
简单的
Logistic回归需调用SAS中LOGISTIC过程完成,一些较复杂的则需要调用CATMOD过程来实现。本节我们重点介绍LOGISTIC过程的用法,通过实例说明如何实现简单的Logistic回归分析。8.5.1 语法格式
|
PROC LOGISTIC [DATA=数据集名] [选项]; |
|
MODEL 应变量名=自变量名列/ [选项]; |
|
[BY <变量名列>; |
|
FREQ <变量名>; |
|
WEIGHT <变量名>; |
|
OUTPUT |
8.5.2 语法说明
LOGISTIC
过程,用最大似然法对应变量拟合一个Logistic模型。除了PROC 和MODEL语句为必需,其他都可省略。【过程选项】
ORDER=DATA|FORMATTED|INTERNAL
DATA :应变量的顺序与数据集中出现的顺序一致
FORMATTED:按照格式化值的顺序,为默认的选项,相当于应变量所赋
值的大小顺序
INTERNAL:按照非格式化值的顺序
-
DESCENDING|DES
颠倒应变量的排列顺序,如果同时指定了选项ORDER,则系统先按照ORDER规定的顺序排列,然后则降序排列。就是说,如果应变量的赋值,死亡为1,存活0,为了得到死亡对存活的概率(或者说是死亡的风险),应选择此选项,否则得到的是存活对死亡的概率。
【MODEL语句】
MODEL语句指定模型的自变量、应变量,模型选项及结果输出选项,如要拟和交互作用项,需先产生一个表示交互作用的新变量。可以拟合带有一个或多个自变量的Logistic回归模型,用最大似然估计法估计模型的参数,打印出模型估计的过程和模型参数的可信区间。
MODEL
语句中常用的选项有:- NOINT 在模型中不拟合常数项,在条件的Logistic回归中用到。
- SELECTION= FORWARD( 或F)| BACKWARD(或B)| STEPWISE|SCORE 规定变量筛选的方法,分别为向前、向后、逐步和最优子集法。缺省时为NONE,拟合全回归模型。
- SLE= 概率值,指定变量进入模型的显著水平,缺省为0.05
- SLS= 概率值,指定变量保留在模型的显著水平,缺省为0.05
- CL|WALDCL ,要求估计所有回归参数的可信区间
- CLODDS=PL|WALD|BOTH , 要求计算OR值的可信区间
- PLRL ,对所有自变量估计OR的可信区间
8.5.3 应用实例
例
8.4 某工作者在探讨肾细胞癌转移的有关临床病理因素研究中,收集了一批行根治性肾切除术患者的肾癌标本资料,现从中抽取26例资料作为示例进行logistic回归分析。表中有关符号意义说明:
i
: 样品序号x
1:确诊时患者的年龄(岁)x2
:肾细胞癌血管内皮生长因子(VEGF),其阳性表述由低到高共3个等级x
3:肾细胞癌组织内微血管数(MVC)x4
:肾癌细胞核组织学分级,由低到高共Ⅳ级x
5:肾细胞癌分期,由低到高共Ⅳ期y
: 肾细胞癌转移情况(有转移y=1; 无转移y=0)。26
例行根治性肾切除术患者的肾癌标本资料
|
i |
X1 |
X2 |
X3 |
X4 |
X5 |
Y |
|
1 |
59 |
2 |
43.4 |
2 |
1 |
0 |
|
2 |
36 |
1 |
57.2 |
1 |
1 |
0 |
|
3 |
61 |
2 |
190.0 |
2 |
1 |
0 |
|
4 |
58 |
3 |
128.0 |
4 |
3 |
1 |
|
5 |
55 |
3 |
80.0 |
3 |
4 |
1 |
|
6 |
61 |
1 |
94.4 |
2 |
1 |
0 |
|
7 |
38 |
1 |
76.0 |
1 |
1 |
0 |
|
8 |
42 |
1 |
240.0 |
3 |
2 |
0 |
|
9 |
50 |
1 |
74.0 |
1 |
1 |
0 |
|
10 |
58 |
3 |
68.6 |
2 |
2 |
0 |
|
11 |
68 |
3 |
132.8 |
4 |
2 |
0 |
|
12 |
25 |
2 |
94.6 |
4 |
3 |
1 |
|
13 |
52 |
1 |
56.0 |
1 |
1 |
0 |
|
14 |
31 |
1 |
47.8 |
2 |
1 |
0 |
|
15 |
36 |
3 |
31.6 |
3 |
1 |
1 |
|
16 |
42 |
1 |
66.2 |
2 |
1 |
0 |
|
17 |
14 |
3 |
138.6 |
3 |
3 |
1 |
|
18 |
32 |
1 |
114.0 |
2 |
3 |
0 |
|
19 |
35 |
1 |
40.2 |
2 |
1 |
0 |
|
20 |
70 |
3 |
177.2 |
4 |
3 |
1 |
|
21 |
65 |
2 |
51.6 |
4 |
4 |
1 |
|
22 |
45 |
2 |
124.0 |
2 |
4 |
0 |
|
23 |
68 |
3 |
127.2 |
3 |
3 |
1 |
|
24 |
31 |
2 |
124.8 |
2 |
3 |
0 |
|
25 |
58 |
1 |
128.0 |
4 |
3 |
0 |
|
26 |
60 |
3 |
149.8 |
4 |
3 |
1 |
本题的应变量为二分类变量,用最简单的
logistic回归模型进行配合,采用逐步筛选法筛选变量,程序如下:|
libname a 'c:\user'; | |
|
data a.bk4_2; | |
|
input x1-x5 y; |
定义X1,X2,X,X4,X5和Y五个变量。 |
|
cards; | |
|
59 2 43.4 2 1 0 | |
|
... | |
|
60 3 149.8 4 3 1 | |
|
proc logistic des; |
选项des指定按照y=1|y=0的 概率来拟合模型 |
|
model y=x1-x5/ selection=stepwise; |
用逐步回归法拟合模型 |
|
run; | |
过程名后面如果不指定选项
DES,则系统按照Y=0的概率拟和模型(Y=0|Y=1),可尝试一下去掉此选项,会发现不仅应变量的排序水平颠倒了,而且所有的参数估计符号相反,OR值为原来的倒数。程序运行的主要输出结果如下:The LOGISTIC Procedure
Data Set: A.BK4_2 计算所用的数据集名
Response Variable: Y 应变量
Response Levels: 2 应变量的水平数
Number of Observations: 26 观察单位数
Link Function: Logit 联系函数Response Profile
Ordered
Value Y Count 1 1 9
2 0 17 根据ORDER和DES选项对应变量的重新排序,给出排序值和及每个水
平相应的例数,拟合排序为1对应的应变量水平的概率 Model Fitting Information and Testing Global Null Hypothesis BETA=0
对模型的总的检验,无效假设为总体的β=0, Intercept
Intercept and
Criterion Only Covariates Chi-Square for CovariatesAIC 35.542 17.826 . SC 36.800 21.600 . -2 LOG L 33.542 11.826 21.716 with 2 DF (p=0.0001)(相当于似然比χ2检验) Score . . 15.844 with 2 DF (p=0.0004)(相当于Pearsonχ2检验)
模型的总的检验,P值均小于0.05,故模型总体有意义。
Analysis of Maximum Likelihood EstimatesParameter Standard Wald Pr> Standardized OddS Variable DF Estimate Error Chi-Square Chi-Square Estimate Ratio 自由度 参数估计 标准误 Waldχ2 P值 标准化回归系数 比值比 INTERCPT 1 -12.3285 5.4305 5.1540 0.0232 . . X2 1 2.4134 1.1960 4.0719 0.0436 1.185510 11.172 X4 1 2.0963 1.0879 3.7131 0.0540 1.230697 8.136
Association of Predicted Probabilities and Observed Responses
预测数和观测数的关联性分析 Concordant = 94.1% Somers' D = 0.902
Discordant = 3.9% Gamma = 0.920
Tied = 2.0% Tau-a = 0.425
(153 pairs) c = 0.951
最后一部分是关于预测概率和观察到的结果的关联性,包括对不同结果的个数和四种秩相关指数的分析。
逐步回归法筛选出两个有意义的变量
X2和X4,其P值都小于0.05,回归系数β分别为2.4134,2.0963,比数比分别为11.172,8.136,事实上,比数比OR=ebeta。据此,写出本例的回归方程如下:LogitP=-12.3285+2.4134X2+2.0963X4。
![]() 上面的方程中X4的P值大于0.05,但没有被剔除出去,这是因为所采用的筛选方法为Stepwise,X4的P值并没有超过剔除标准,因此仍在方程内。结合专业,最终的方程仍然保留了X4。
上面的方程中X4的P值大于0.05,但没有被剔除出去,这是因为所采用的筛选方法为Stepwise,X4的P值并没有超过剔除标准,因此仍在方程内。结合专业,最终的方程仍然保留了X4。
本例用逐步回归法筛选出对患肾细胞癌有意义的危险因素有两个,肾细胞癌血管内皮生长因子
(VEGF)的等级越高,肾癌细胞核组织学分级越高,患肾细胞癌的危险越大。比较两个标准化回归系数,X2对于患肾细胞癌的影响要大于X4。
(原著:田晓燕)
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言






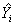
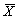




#Logistic#
64
#SAS#
70
#logistic回归#
58
#GIST#
75