SPSS教程第九课:回归分析
2012-04-12 生物谷 生物谷
回归分析是处理两个及两个以上变量间线性依存关系的统计方法。在医学领域中,此类问题很普遍,如人头发中某种金属元素的含量与血液中该元素的含量有关系,人的体表面积与身高、体重有关系;等等。回归分析就是用于说明这种依存变化的数学关系。 第一节 Linear过程 8.1.1 主要功能 调用此过程可完成二元或多元的线性回归分析
回归分析是处理两个及两个以上变量间线性依存关系的统计方法。在医学领域中,此类问题很普遍,如人头发中某种金属元素的含量与血液中该元素的含量有关系,人的体表面积与身高、体重有关系;等等。回归分析就是用于说明这种依存变化的数学关系。
第一节 Linear过程
8.1.1 主要功能
调用此过程可完成二元或多元的线性回归分析。在多元线性回归分析中,用户还可根据需要,选用不同筛选自变量的方法(如:逐步法、向前法、向后法,等)。
8.1.2 实例操作
[例8.1]某医师测得10名3岁儿童的身高(cm)、体重(kg)和体表面积(cm2)资料如下。试用多元回归方法确定以身高、体重为自变量,体表面积为应变量的回归方程。
|
儿童编号 |
体表面积(Y) |
身高(X1) |
体重(X2) |
|
1 2 3 4 5 6 7 8 9 10 |
5.382 5.299 5.358 5.292 5.602 6.014 5.830 6.102 6.075 6.411 |
88.0 87.6 88.5 89.0 87.7 89.5 88.8 90.4 90.6 91.2 |
11.0 11.8 12.0 12.3 13.1 13.7 14.4 14.9 15.2 16.0 |
8.1.2.1 数据准备
激活数据管理窗口,定义变量名:体表面积为Y,保留3位小数;身高、体重分别为X1、X2,1位小数。输入原始数据,结果如图8.1所示。

图8.1 原始数据的输入
8.1.2.2 统计分析
激活Statistics菜单选Regression中的Linear...项,弹出Linear Regression对话框(如图8.2示)。从对话框左侧的变量列表中选y,点击Ø钮使之进入Dependent框,选x1、x2,点击Ø钮使之进入Indepentdent(s)框;在Method处下拉菜单,共有5个选项:Enter(全部入选法)、Stepwise(逐步法)、Remove(强制剔除法)、Backward(向后法)、Forward(向前法)。本例选用Enter法。点击OK钮即完成分析。

用户还可点击Statistics...钮选择是否作变量的描述性统计、回归方程应变量的可信区间估计等分析;点击Plots...钮选择是否作变量分布图(本例要求对标准化Y预测值作变量分布图);点击Save...钮选择对回归分析的有关结果是否作保存(本例要求对根据所确定的回归方程求得的未校正Y预测值和标准化Y预测值作保存);点击Options...钮选择变量入选与剔除的α、β值和缺失值的处理方法。
8.1.2.3 结果解释
在结果输出窗口中将看到如下统计数据:
|
* * * * M U L T I P L E R E G R E S S I O N * * * * Listwise Deletion of Missing Data Equation Number 1 Dependent Variable.. Y Block Number 1. Method: Enter X1 X2 Variable(s) Entered on Step Number 1.. X2 2.. X1 Multiple R .94964 R Square .90181 Adjusted R Square .87376 Standard Error .14335 Analysis of Variance DF Sum of Squares Mean Square Regression 2 1.32104 .66052 Residual 7 .14384 .02055 F = 32.14499 Signif F = .0003 ------------------ Variables in the Equation ------------------ Variable B SE B Beta T Sig T X1 .068701 .074768 .215256 .919 .3887 X2 .183756 .056816 .757660 3.234 .0144 (Constant) -2.856476 6.017776 -.475 .6495 End Block Number 1 All requested variables entered. |
结果显示,本例以X1、X2为自变量,Y为应变量,采用全部入选法建立回归方程。回归方程的复相关系数为0.94964,决定系数(即r2)为0.90181,经方差分析,F=34.14499,P=0.0003,回归方程有效。回归方程为Y=0.0687101X1+0.183756X2-2.856476。
本例要求按所建立的回归方程计算Y预测值和标准化Y预测值(所谓标准化Y预测值是指将根据回归方程求得的Y预测值转化成按均数为0、标准差为1的标准正态分布的Y值)并将计算结果保存入原数据库。系统将原始的X1、X2值代入方程求Y值预测值(即库中pre_1栏)和标准化Y预测值(即库中zpr_1栏),详见图8.3。

图8.3 计算结果的保存
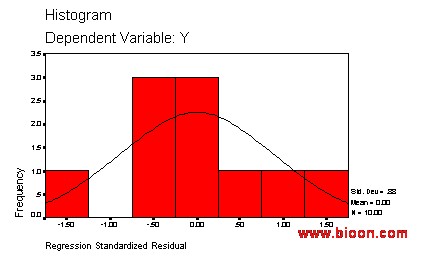
本例还要求对标准化Y预测值作变量分布图,系统将绘制的统计图送向Chart Carousel窗口,双击该窗口可见下图显示结果。

图8.4 对标准化Y预测值所作的正态分布图
第二节 Curve Estimation过程
8.2.1 主要功能
调用此过程可完成下列有关曲线拟合的功能:
1、Linear:拟合直线方程(实际上与Linear过程的二元直线回归相同,即Y = b0+ b1X);
2、Quadratic:拟合二次方程(Y = b0+ b1X+b2X2);
3、Compound:拟合复合曲线模型(Y = b0×b1X);
4、Growth:拟合等比级数曲线模型(Y = e(b0+b1X));
5、Logarithmic:拟合对数方程(Y = b0+b1lnX)
6、Cubic:拟合三次方程(Y = b0+ b1X+b2X2+b3X3);
7、S:拟合S形曲线(Y = e(b0+b1/X));
8、Exponential:拟合指数方程(Y = b0 eb1X);
9、Inverse:数据按Y = b0+b1/X进行变换;
10、Power:拟合乘幂曲线模型(Y = b0X b1);
11、Logistic:拟合Logistic曲线模型(Y = 1/(1/u + b0×b1X)。
8.2.2 实例操作
[例8.2]某地1963年调查得儿童年龄(岁)X与锡克试验阴性率(%)Y的资料如下,试拟合对数曲线。
|
年龄(岁) X |
锡克试验阴性率(%) Y |
|
1 2 3 4 5 6 7 |
57.1 76.0 90.9 93.0 96.7 95.6 96.2 |
8.2.2.1 数据准备
激活数据管理窗口,定义变量名:锡克试验阴性率为Y,年龄为X,输入原始数据。
8.2.2.2 统计分析
激活Statistics菜单选Regression中的Curve Estimation...项,弹出Curve Estimation对话框(如图8.5示)。从对话框左侧的变量列表中选y,点击Ø钮使之进入Dependent框,选x,点击Ø钮使之进入Indepentdent(s)框;在Model框内选择所需的曲线模型,本例选择Logarithmic模型(即对数曲线);选Plot models项要求绘制曲线拟合图;点击Save...钮,弹出Curve Estimation:Save对话框,选择Predicted value项,要求在原始数据库中保存根据对数方程求出的Y预测值,点击Continue钮返回Curve Estimation对话框,再点击OK钮即可。

8.2.2.3 结果解释
在结果输出窗口中将看到如下统计数据:
|
ndependent: X Dependent Mth Rsq d.f. F Sigf b0 b1 Y LOG .913 5 52.32 .001 61.3259 20.6704 |
在以X为自变量、Y为应变量,采用对数曲线拟合方法建立的方程,决定系数R2=0.913(接近于1),作拟合优度检验,方差分析表明:F=52.32,P=0.001,拟合度很好,对数方程为:Y=61.3259+20.6704lnX。
本例要求绘制曲线拟合图,结果如图8.6所示。

图8.6 对数曲线拟合情形

图8.7 计算结果的保存
第三节 Logistic过程
8.3.1 主要功能
调用此过程可完成Logistic回归的运算。所谓Logistic回归,是指应变量为二级计分或二类评定的回归分析,这在医学研究中经常遇到,如:死亡与否(即生、死二类评定)的概率跟病人自身生理状况和所患疾病的严重程度有关;对某种疾病的易感性的概率(患病、不患病二类评定)与个体性别、年龄、免疫水平等有关。此类问题的解决均可借助逻辑回归来完成。
特别指出,本节介绍的Logistic过程,应与日常所说的Logistic曲线模型(即S或倒S形曲线)相区别。用户如果要拟合Logistic曲线模型,可调用本章第二节Curve Estimation过程,系统提供11种曲线模型,其中含有Logistic曲线模型(参见上节)。
在一般的多元回归中,若以P(概率)为应变量,则方程为P=b0+b1X1+b2X2+…+bkXk,
但用该方程计算时,常会出现P>1或P<0的不合理情形。为此,对P作对数单位转换,即logitP=ln(P/1-P),于是,可得到Logistic回归方程为:
eb0+b1X1+b2X2+…+bkXk
P = ———————————
1+ eb0+b1X1+b2X2+…+bkXk
8.3.2 实例操作
[例8.3]某医师研究男性胃癌患者发生术后院内感染的影响因素,资料如下表,请通过Logistic回归统计方法对主要影响因素进行分析。
|
术后感染 (有无) Y |
年龄 (岁) X1 |
手术创伤程度 (5等级) X2 |
营养状态 (3等级) 小提示:本篇资讯需要登录阅读,点击跳转登录
版权声明:
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。 在此留言 相关资讯SPSS教程第七课:方差分析方差分析是R.A.Fister发明的,用于两个及两个以上样本均数差别的显著性检验。由于各种因素的影响,研究所得的数据呈现波动状,造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。方差分析的基本思想是:通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。 方差分析主要用于:1、均数 SPSS教程第八课:相关分析任何事物的存在都不是孤立的,而是相互联系、相互制约的。在医学领域中,身高与体重、体温与脉搏、年龄与血压等都存在一定的联系。说明客观事物相互间关系的密切程度并用适当的统计指标表示出来,这个过程就是相关分析。 值得注意,事物之间有相关,不一定是因果关系,也可能仅是伴随关系。但如果事物之间有因果关系,则两者必然相关。 SPS 第三课:SPSS的数据管理统计分析离不开数据,因此数据管理是SPSS的重要组成部分。详细了解SPSS的数据管理方法,将有助于用户提高工作效率。SPSS的数据管理是借助于数据管理窗口和主窗口的File、Data、Transform等菜单完成的。 第一节 数据的输入 2.1.1 变量的定义 先激活数据管理窗口,然后选Data菜单的Define Variable. 第四课:SPSS文本文件的编辑上一章介绍了SPSS数据管理窗口的使用方法。在第一章中,我们还提到过SPSS的其他窗口,如结果输出窗口(图3.1)和命令编辑窗口(图3.2),这两个窗口是系统用于接收或输出文本的。用户经常在实际工作中需要对之进行必要的编辑。SPSS的文本编辑是借助于主窗口的File、Edit等菜单完成的,本章介绍SPSS的文本编辑方法。 第一节 文本文件 第五课:摘要性分析摘要性分析是对原始数据进行描述性分析,这是统计工作的出发点。统计学的一系列基本描述指标,不仅让人了解资料的特征,而且可启发人们对之作进一步的深入分析。通过调用摘要性分析的诸个过程,可完成许多统计学指标,对于计量资料,可完成均数、标准差、标准误等指标的计算;对于计数和一些等级资料,可完成构成比、率等指标的计算和χ2 检验。本章将介绍其操作方法。 第一节 Frequenci SPSS教程第六课:平均数的比较在正态或近似正态分布的计量资料中(如临床常见的体温、血压、脉搏、身高、体重等测量值,几乎均为此类资料),经常在使用前一章计量资料描述过程分析后,还要进行组与组之间平均水平的比较。本章将分四节分别介绍这一统计方法:即常用的t检验和单因素方差分析。 第一节 Means过程 5.1.1 主要功能 &nbs |












#回归分析#
61